基本思想
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治策略。
- 分
将问题分(divide)成一些小的问题然后递归求解
- 治
则将分的阶段得到数据进行加工处理,最终形成一个有顺序的序列,这就是分而治之
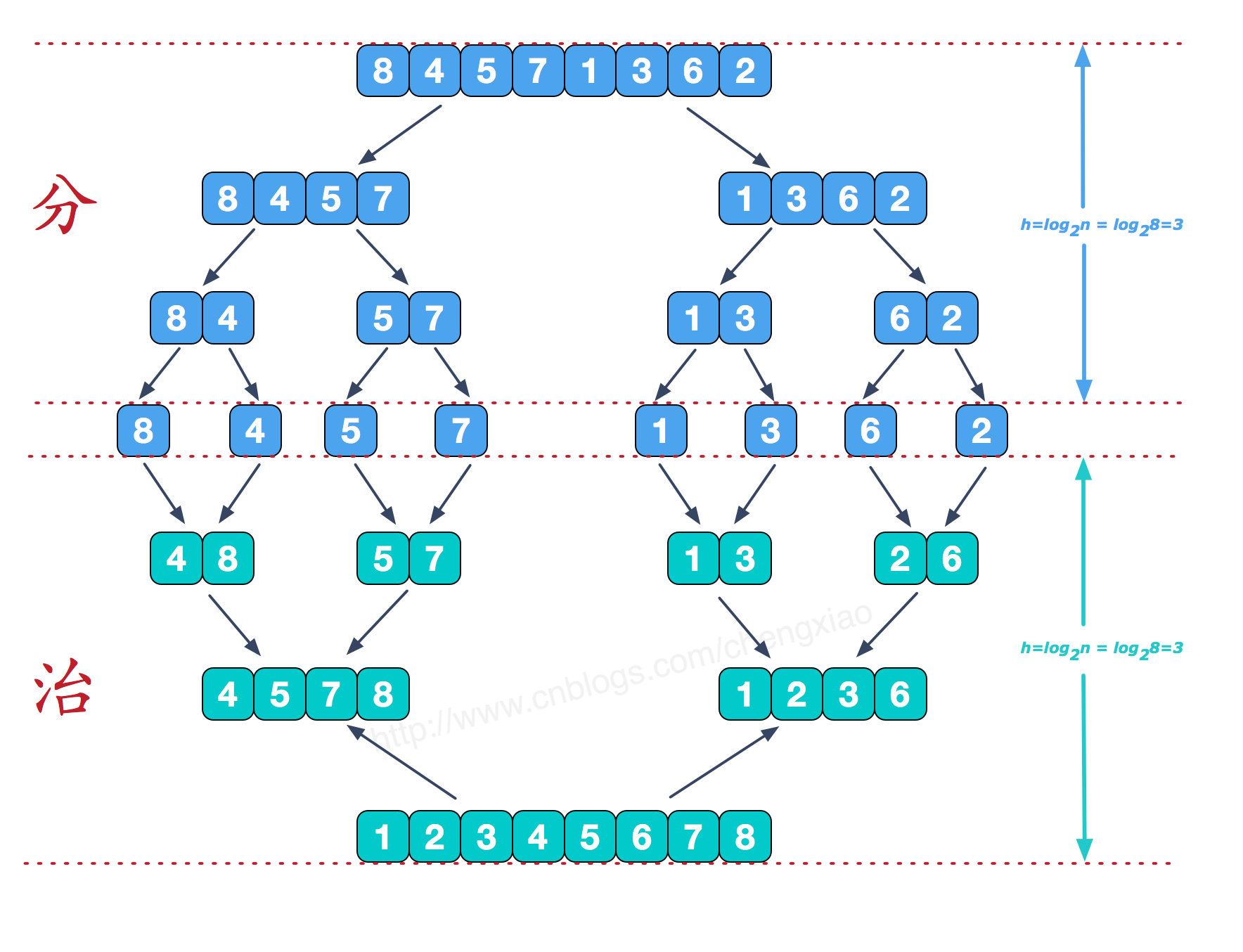
可以看到这种结构很像一棵完全二叉树,归并排序可以使用迭代、递归的方式去实现,这里采用递归;
合并相邻序列
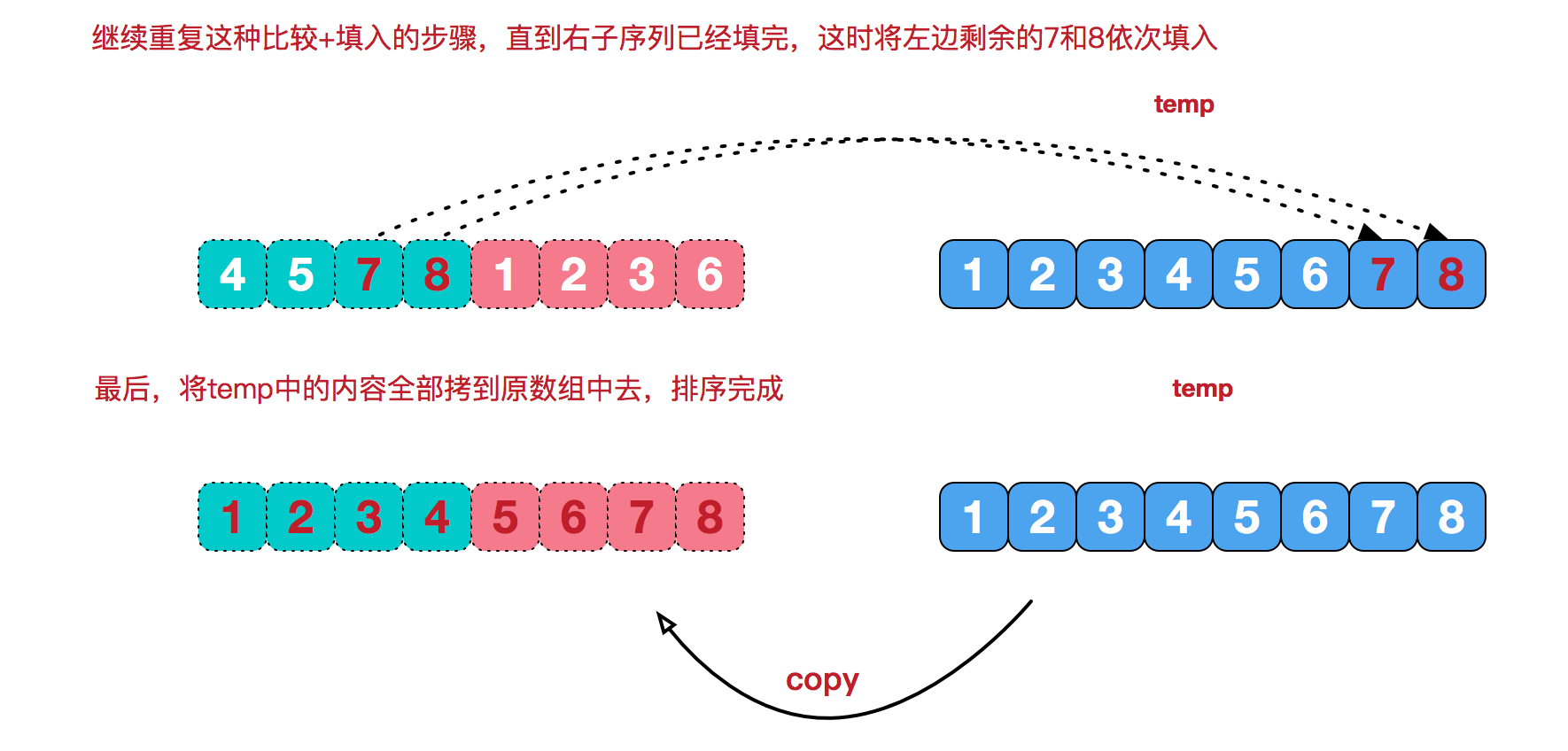
再来看看治阶段,将两个已经有序的子序列合并成一个有序序列,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],实现步骤:
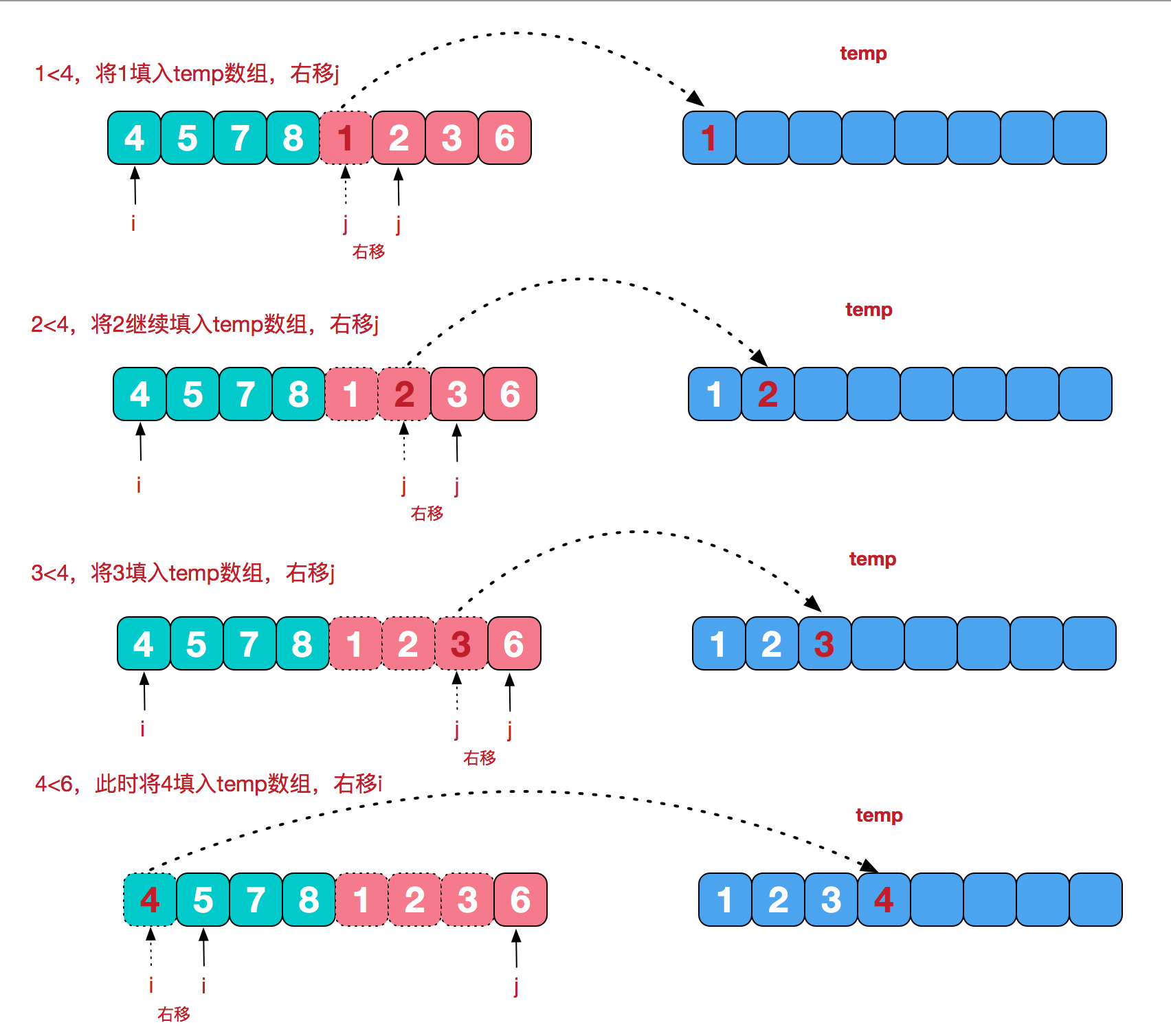
代码实现
package com.ikonke.openapi;
import java.util.Arrays;
public class Test2 {
public static void main(String[] args) {
int[] arr = {9, 8, 7, 6, 5, 4, 3, 2, 1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
/**
* 排序递归的方法
*
* @param arr
*/
public static void sort(int[] arr) {
/**
* 临时数组
*/
int[] temp = new int[arr.length];
sort(arr, 0, arr.length - 1, temp);
}
/**
* 分治的方法
*
* @param arr
* @param left
* @param right
* @param temp
*/
private static void sort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
//从数组中间开始
int mid = (left + right) / 2;
//左边归并排序,使得左子序列有序
sort(arr, left, mid, temp);
//右边归并排序,使得右子序列有序
sort(arr, mid + 1, right, temp);
//将两个有序子数组合并操作
merge(arr, left, mid, right, temp);
}
}
/**
* 数组合并
*
* @param arr 原数组
* @param left
* @param mid
* @param right
* @param temp 临时数组
*/
private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left;//左指针
int j = mid + 1;//右指针
int t = 0;//临时数组指针
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
while (i <= mid) {//将左边数组赋值到临时数组
temp[t++] = arr[i++];
}
while (j <= right) {//将右边数组赋值到临时数组
temp[t++] = arr[j++];
}
t = 0;
//数组拷贝替换
while (left <= right) {
arr[left++] = temp[t++];
}
}
}
执行结果
[1, 2, 3, 4, 5, 6, 7, 8, 9]
总结
归并排序是稳定排序,也是一种十分高效的排序,当进行大数据排序的时候使用归并效率会高很多,如果只有>50个数组,我认为还是使用插入排序、冒泡排序之类的,会合适些。
从上文的图中可看出,每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且,归并排序的最好,最坏,平均时间复杂度均为O(nlogn)。


近期评论